Cem ERSU

Unboxing the Black Box. Deconstructing AI algorithms with Math & Python.

1 minute read

Welcome to the lab. 🧪

Sometimes, looking at typed formulas on a screen feels too abstract. To truly understand concepts like Variance or Outlier Detection, I have to turn off the computer, grab my tablet, and scribble them down manually.

This week, I revisited the core pillars of data distribution. Here are my raw field notes.

1. The Battle of Variances: Biased vs. Unbiased

When I first learned variance, I was confused. Why do we sometimes divide by n and sometimes by n-1?

I drew this out to make it stick:

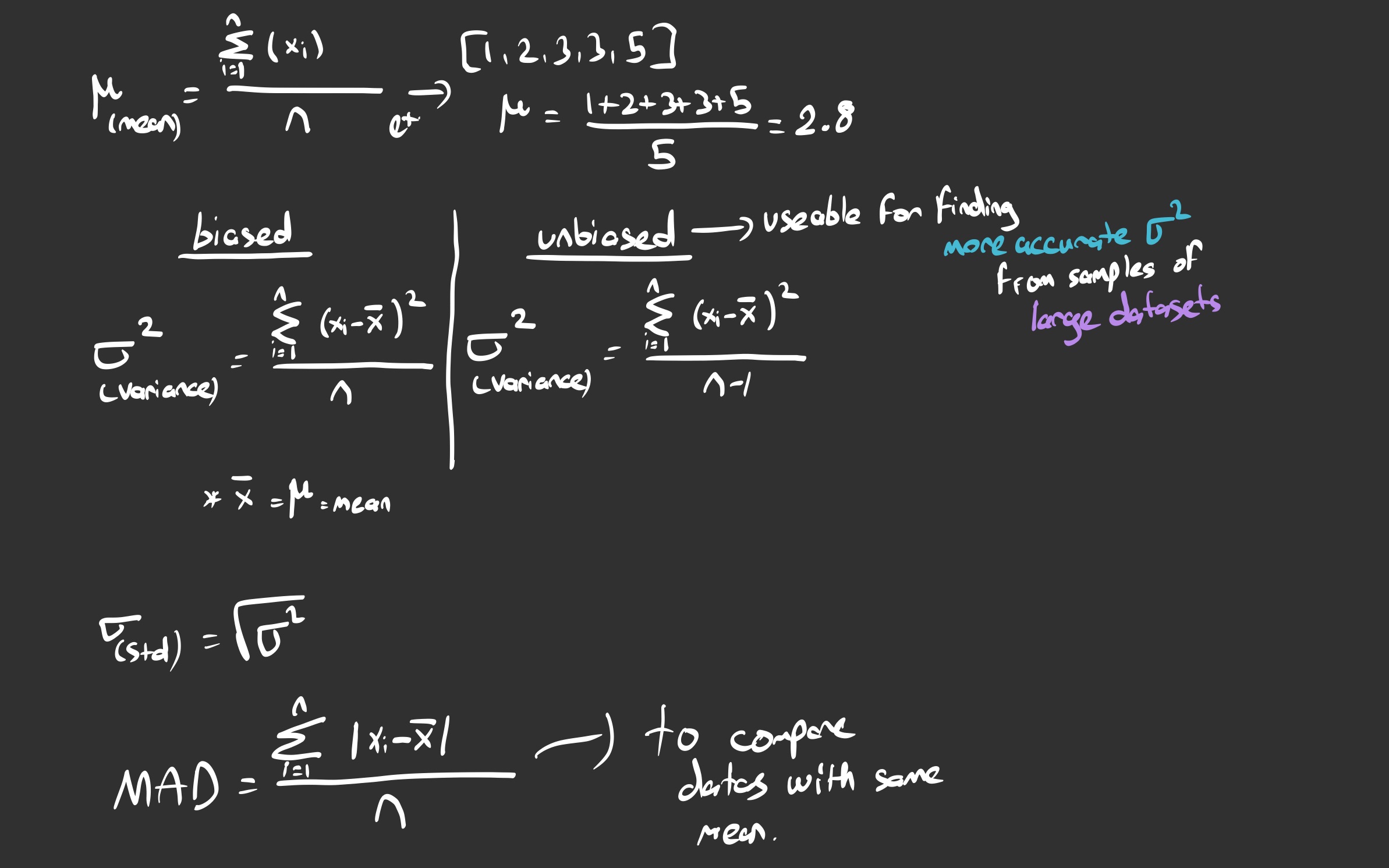
Variance and Standard Deviation Notes

My Key Takeaways:

  • The Mean (μ): This is just the center of gravity. In my example [1, 2, 3, 3, 5], the mean sits at 2.8.
  • Biased Variance (Dividing by n): This assumes we have data for the entire population.
  • Unbiased Variance (Dividing by n-1): This is the crucial part for Data Science. Since we usually work with samples (small chunks of big data), dividing by n underestimates the error. Dividing by n-1 corrects this bias.
    • Note to self: Always check if I’m working with a sample or the full population before writing the code!
  • MAD: As noted at the bottom, Mean Absolute Deviation is great for comparing datasets with the same mean, but Variance is mathematically more potent.

2. Spotting the Anomalies: The Box Plot

In any experiment (or when tracking my own bio-data), anomalies happen. A sensor glitches, or I have a surprisingly bad sleep score. How do we scientifically decide what is “normal” and what is an “outlier”?

Enter the Box Plot and the 1.5 IQR Rule.

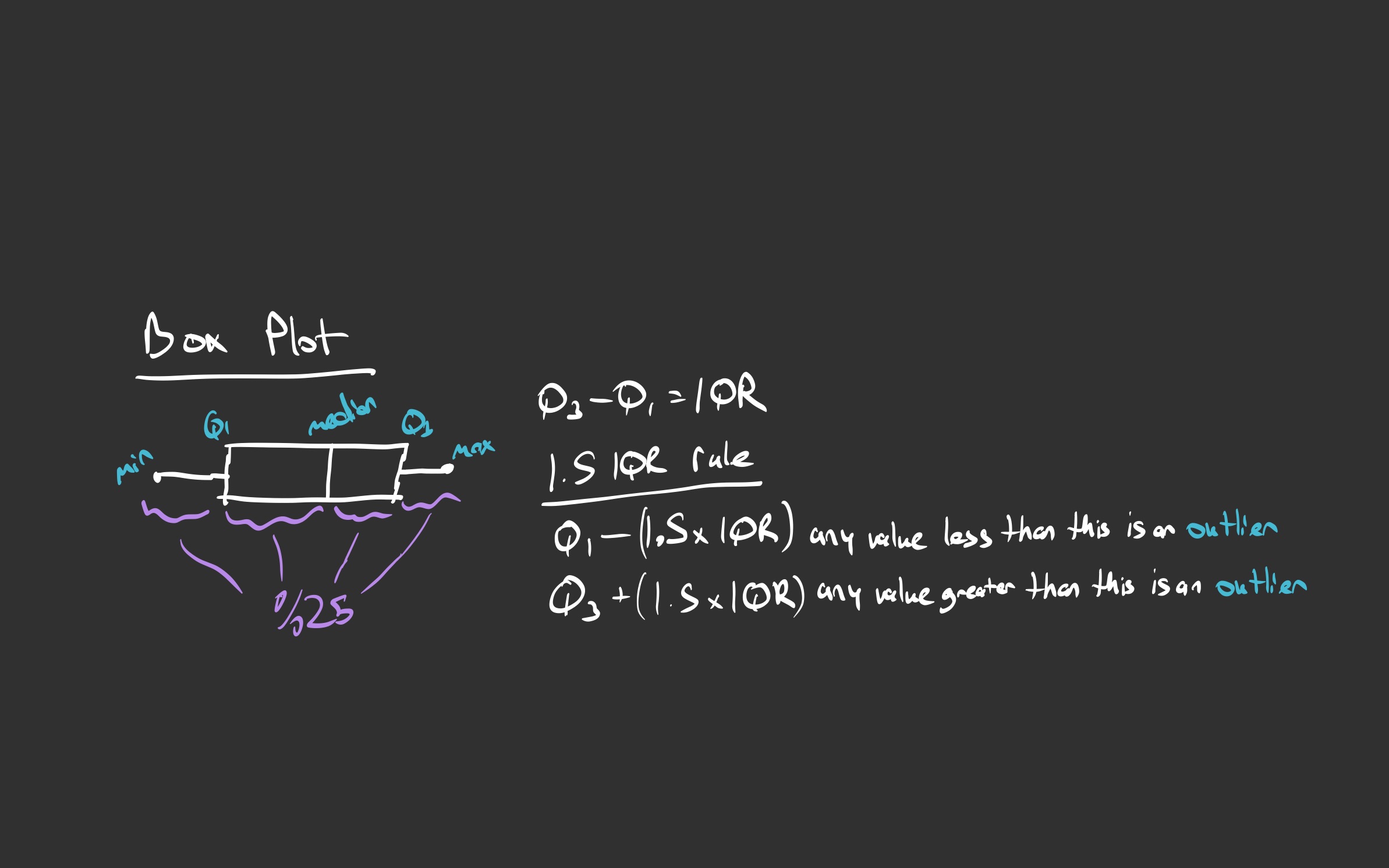
Box Plot and IQR Rule Notes

The Logic:

  1. The Box: Represents the middle 50% of the data.
  2. IQR (Interquartile Range): The distance between Q3 (75th percentile) and Q1 (25th percentile).
  3. The Whisker Limits:
    • The “safe zone” ends at 1.5 x IQR.
    • Anything beyond the whiskers (the purple lines in my sketch) is officially an Outlier.

Conclusion

Writing these down by hand helped me visualize the “geometry” of data.

  • Variance is about the spread (squared).
  • Box Plots are about the boundaries.

Next time you see a complicated formula, try drawing it. It changes everything.

You May Also Enjoy